
Why Do Atoms Radiate Light?
Light has undoubtedly been one of the most interesting natural phenomena throughout human history. The structure of light has been one of the most debated issues throughout the history of science, and whether it behaves like a wave or as a particle has always been the cause of heated debates. Sunlight that keeps our daily lives going, lamps that illuminate us in the dark, lasers that are used in many scientific researches and in the entertainment industry, and also the spectroscopic methods we use in chemical investigations are all possible as a result of the radiations made by atoms/molecules.
But why do atoms radiate light? How can we understand this radiation process and how can we put it in a theoretical framework? These questions are an inevitable requirement, as well as a practical consequence, of our understanding of light and atomic structure. Then, let’s get started!
The Transition from High Energy to Low: Radiation
If you’ve read up to this point, you probably think you know the answer to the question of why atoms glow. At one point in our education, they told us that electrons radiate as a result of falling from high energy levels to low energy levels and that a photon with an energy equal to the difference between these two energy levels is produced. Likewise, they explained that the energy levels in atoms are stable orbits and that the electrons in these areas will continue to be there forever if they are not disturbed. Well, if these orbitals are stable and it can be calculated that the electrons must be there for an infinite amount of time, why do the electrons move to lower energies?

An Atom Conception That Could Cause Infinite Darkness: Let Sleeping Dogs Lie
To the question I asked above, to be honest, I couldn’t find an answer at first either. But later, when I learned the answer, I thought that I should share it with everyone (in fact, there is no answer, it is something you can find when you go through the books). The answer to the question is hidden in the sentence I set up above: “they will continue to be there if they are not disturbed”. This point explains why atoms actually radiate. However, I will start from the beginning and try to explain the phenomenon of radiation as broadly as possible, but at the same time simple.

Atoms, as we all know, generally consist of a positively charged nucleus filled with protons and neutrons and negatively charged electrons orbiting around it. Of course, these electrons do not randomly orbit the nucleus; Certain energy levels and the corresponding orbitals are the places where electrons are most likely to be found, and we can practically say that electrons travel in these orbitals. These orbits correspond mathematically to the solutions of the Schrödinger equation for different energy values. In the language of chemists, 1s, 2s, 3s orbitals always mean solutions of the same equation for different energies.
No Reason to Glow (!)
Since the energies of each of the orbitals are different from each other (for example, 1s and 2p), the transition of an electron wandering in 2p to 1s means that a photon equal to the difference between the two energy levels emerges, which we call “light” and the phenomenon we call “radiation”. Of course, the spontaneous transition of the electron from 2p to 1s at this time does not seem unusual or incomprehensible to us. After all, it is a phenomenon that we see all the time, it has a usual explanation, and therefore there is no problem for us. But actually, the main problem arises here; there is no reason for an electron to spontaneously transition from 2p to 1s as we learned!

Those who have taken the quantum mechanics course will remember it immediately, for those who have not, I will try to explain. The solutions of the Schrödinger equation corresponding to different energies are called stationary states. This means that when you put your particle in an orbit that is one of the solutions of the Schrödinger equation, the particle will continue to be there indefinitely because the probability of transitioning to other orbits over time will be “0”*. So why do atoms radiate? Is there something wrong with quantum mechanics? Did we learn wrong? Did they trick us?
The gist of the matter is that unfortunately there is no answer to this question in “classical quantum mechanics”, which is shaped around the Schrödinger equation. More precisely, Schrödinger tells us that the answer is 0, so there can be no transition. But of course, there are other factors that he did not take into account, and we need to take these effects into account.
Energy Fluctuations in the Electromagnetic Field
Remember electricity and magnetism. They told us about these two phenomena both in high school and at university. We know that an electrically charged particle will create an electric field around it, and if this particle moves, a magnetic field will be created. What we always remember in these two phenomena, which we have gathered under the name of electromagnetic, is the existence of magnetic and electric fields. When we say space, we always think of an environment; a structure with no holes or cuts on it, just like a sheet. However, the electromagnetic field has a discontinuous structure, just like the energy levels of atoms. The theory, called quantum electrodynamics, gives us a way to unify the classical electromagnetic field with quantum mechanics, and according to this theory, the electromagnetic field also has discrete values. Moreover, there are many energy fluctuations in the electromagnetic field at any moment** (even in a vacuum where there are no particles!) and these energy fluctuations are responsible for the radiation of our atoms.

Yes, it’s a bit complicated and unexpected.
So how’s it going? We took one atom, and let it be the hydrogen atom for convenience. We also put the single electron of the atom in the second energy level. Normally, if there were no energy fluctuations even in vacuum, this electron would stay here forever (sure, it will). But the fluctuations of the electromagnetic field make all orbitals unstable except the first energy level (i.e. the 1s orbit). Hence, the second, third, … energy levels are no longer a solution to the Schrödinger equation. They still may be approximate solutions, but approximate does not mean complete and exact. That’s why electrons in other energy levels are no longer in a stable orbit and fall into the first energy level, which is the only stable energy level.

So, we have to put a lot of things on top of classical quantum mechanics to understand this situation.
Another question may come to mind here. What would happen if our atom was not hydrogen but lithium? There are three electrons in a lithium atom, and one of them is in the second energy level. Then wouldn’t this electron have to fall to the first energy level as well? If the Pauli Principle did not exist, that is, if more than two electrons could share the same orbital, this would of course also happen.
If We Need To Sum Up…
Let me summarize briefly what I have said so far. Electrons orbit the nucleus in orbits of different energies, but these orbits are not stable orbits due to energy fluctuations in the electromagnetic field. Therefore, electrons, if possible, go to lower energy levels, and during this transition, they cause the emergence of a photon with an energy equal to the energy difference between them. These photons correspond to what we basically call light. Scientifically, these transitions are also called spontaneous transition, or spontaneous radiation (in fact, it does not happen spontaneously at all, this is a name that has historically settled in our language).
Basic Transition Rules
Of course, the transitions between orbits cannot be so random. For example, you do not have a chance to go from the 5p orbital to the 1s orbital in one go. Or in certain situations, you cannot switch from the 3s orbital to the 2s orbital. All these prohibited-permitted transitions are gathered under the name of “selection rules“.
I want to examine two very basic transition rules and end the article. The first of these is the Laporte transition rule. Laporte’s transition rule states that transitions such as s-s, p-p, and d-d are forbidden in centrally symmetric molecules, that is, molecules with a symmetry point at the center of the molecule. In more mathematical language, transitions between two double orbitals (gerade) or two single orbitals (ungerade) are prohibited. This is because of the integrals used when calculating each transition probability. More plainly, if you want to calculate the u-u or g-g transition probabilities, your result will always be zero.
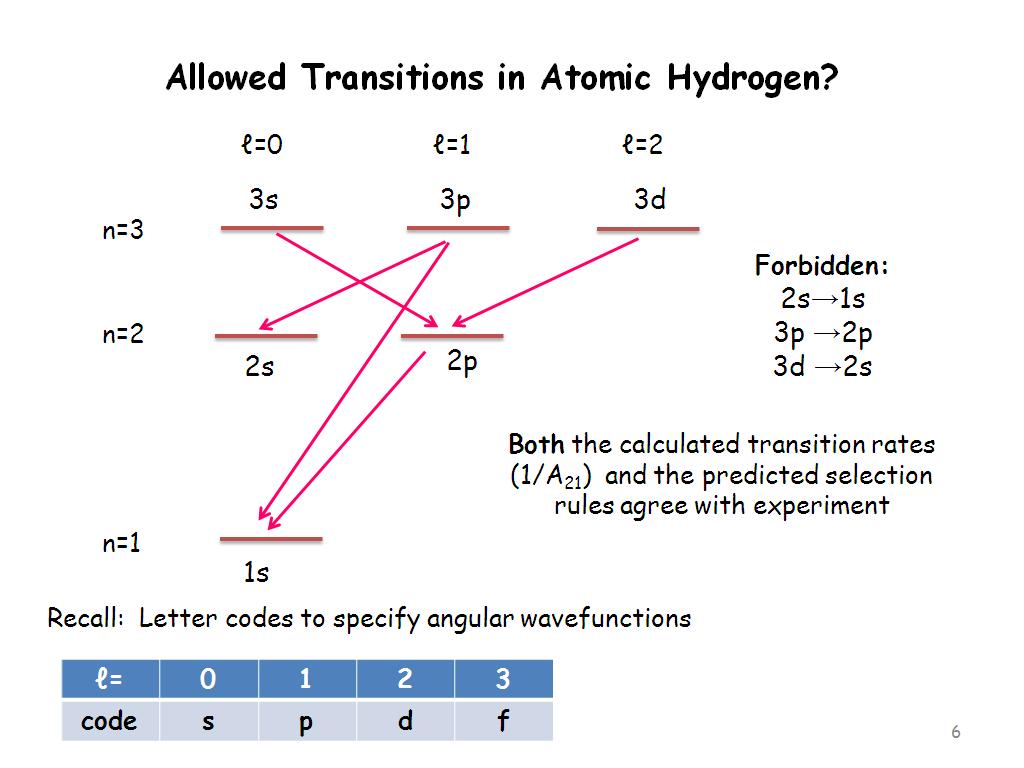
Image Source: Nanohub.org
But does Laporte’s rule apply to every central symmetric molecule, are there exceptions? Laporte’s rule applies primarily to centrally symmetric molecules. However, since this symmetry is broken, that is, the molecule becomes more asymmetrical, Laporte-forbidden transitions are possible. This effect is also called the Jahn-Teller effect.
Moreover, although the symmetry of the molecule is not broken, there is a possibility of transition. Since the fluctuations in the electromagnetic field that I mentioned in the first part of the article make the orbitals in the upper energy levels more unstable, these transitions can happen from time to time. This is the main reason why signals corresponding to the Laporte-forbidden regions can be found, albeit very weakly, in the measured spectra.
The second rule I want to mention is that in electronic transitions, the magnetic quantum number should either decrease or increase slightly or not change at all; all remaining transitions are prohibited (Δm=0,1,-1). This rule basically says that you can’t always go from f orbitals to s orbitals in one step. I have reserved the very simple reason for this in the last paragraph.
Conservation of Angular Momentum
We know that a photon is emitted in electronic transitions. Of course, the total angular momentum (the value that kind of describes the rotation of the system) has to be conserved. Photons have an angular momentum magnitude of 1, so the number m of any photon can be -1, 0, or 1 (remember, m ranges from +l to -l). If we want to conserve the total angular momentum, then our transition must also change the value m by -1, 0, or 1, otherwise, we have no chance of conserving the angular momentum. In short, this transition rule also depends on a very basic principle, the conservation of angular momentum.

Thus, I come to the end of the article. I tried to explain the emergence of light and why atoms radiate. Contrary to what we generally know, I tried to mention that there is no such simple reason for this radiation phenomenon and that radiation is possible due to the intermittent electromagnetic field and the fluctuations that occur here. Finally, I talked about the reasons for some transition rules that chemists often use, especially in inorganic chemistry and spectroscopy. Of course, there are many more transition rules. These, however, are the subject of another article.
Notes:
* The solutions of the Schrödinger equation are orthogonal to each other. In this case, the overlap between any two orbitals has to be 0.
** Quantum electrodynamics is the discrete study of the electromagnetic field. That is, the fields are not continuous, but discrete. The energy fluctuations occurring in this field are also a result of the Heisenberg uncertainty principle.
References and Further Reading
Hydrogen Atom Radiation. NanoHUB.org – courses: PHYS 342: Modern physics: Public self-paced. (n.d.). Retrieved September 28, 2021, from https://nanohub.org/courses/phys342/public_v1/outline/week6hydrogenatom-radiation/l66allowedtransitionsselectionrulesandlasers.
Libretexts. (2020, August 15). Selection rules and Transition moment integral. Chemistry LibreTexts. Retrieved September 28, 2021, from https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Spectroscopy/Fundamentals_of_Spectroscopy/Selection_rules_and_transition_moment_integral.
Images not cited are used through Canva Pro with a royalty payment.
The proofreading has been done by Asu Pelin Akköse and Mete Esencan.
Would you like to support us?
- For more detailed information, you can check our “Support Us!” page!







